Introduction
I have worked on different types of physical problems through my carrier. Most of them can be classified into four big groups. The problems of strongly correlated systems define the first one. My doctoral and undergraduate research was devoted to this field. It was focused mainly on the problem of spin and charge orderings in Hubbard-like models and related phase and valence transitions in these systems.The second group is the study of stochastic dynamics in the systems with various tilted potentials. These studies had been motivated by the superconducting phase dynamics and properties of the noise in unconventional Josephson junctions, but have a much broader applicability.
The third group of problems is dealing with the quantum dot attached to superconducting leads. Such heterostructures are in principle generalized and tunable Jusephson juncions with enormous potential in electronics and quantum computing.
The fourth group consists of different projects focused on the time evolution of quantum systems. These projects demand Master equation approach or some modern real-time quantum Monte Carlo algorithms. I am currently learning a lot about these systems and methods, meaning that I am trying to write some solvers.
I am also involved in other projects including a study focused on the laser induced superdifusion in the magnetic heterostructures and in the theoretical analysis of recent spectroscopic experiments on the organic molecule/metal structures.
Stochastic dynamical systems
The stochastic dynamic motion of a particle in tilted periodic potential plays an important role in the studies of various physical phenomena including Josephson junctions, micro-particles confined in shaped laser beams, dynamics of charge density waves, crystal surface melting as well as for different biophysical processes. A well paid off effort has been already invested into the theoretical analysis of such systems, nevertheless, the interest is not fading. In contrary, the recent experimental progress in different fields calls for explanation of new phenomena as well as for readdressing of some old problems.We are primarily interested in the phase dynamics of the Josephson junctions. The Josephson junctions are superconducting electronic devices used in extremely sensitive magnetometers and voltmeters and also a promising candidates for the basic circuit elements of the future quantum computers. We have find out, that the overall voltage noise of this devices, despite its bad reputation, can be a very useful property. It carries a lot of information on the phase dynamics of the device. we elaborated a sophisticated numerical method to extract this information. This method can be used to calculate rates of different elementary phase processes directly from the noise.
Voltage noise of Josephson Junction
We study the voltage noise properties including the switching rates and statistics of the phase-slips
in moderately damped Josephson junctions using an efficient numerical approach
combining the matrix continued-fraction method with the full counting statistics.
We identify different dominating components, namely the thermal noise close to equilibrium
(small current-bias regime), the shot noise of (multiple) phase-slips in the intermediate
range of biases and the switching noise for yet higher bias currents.
We extract characteristic rates of phase-slips in the shot noise regime as well as the escape
and retrapping rates in the switching regime as functions of various junction's parameters.
We also study the influence of different electrodynamic environments on the phase dynamics.
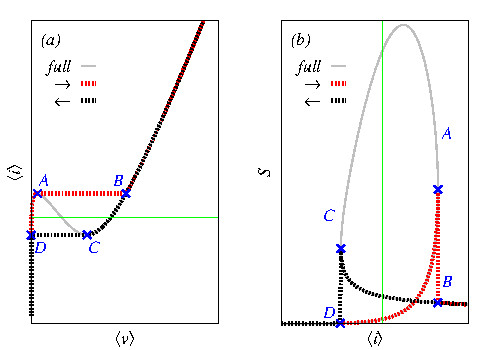
The figure represents an illustrative explanation of the discontinuous drops in I-V characteristics and voltage noise (S)
measured in experiments. They are a consequence of the environment and the measurement protocol.Related publications:[1][2]
Phase dynamics of Josephson Junction with second harmonic in CPR
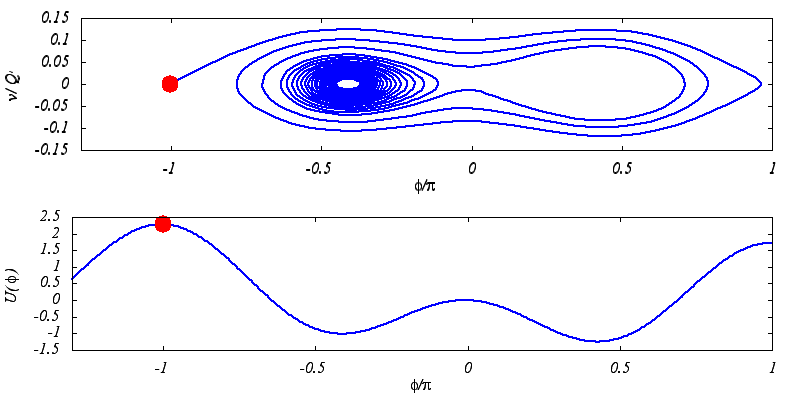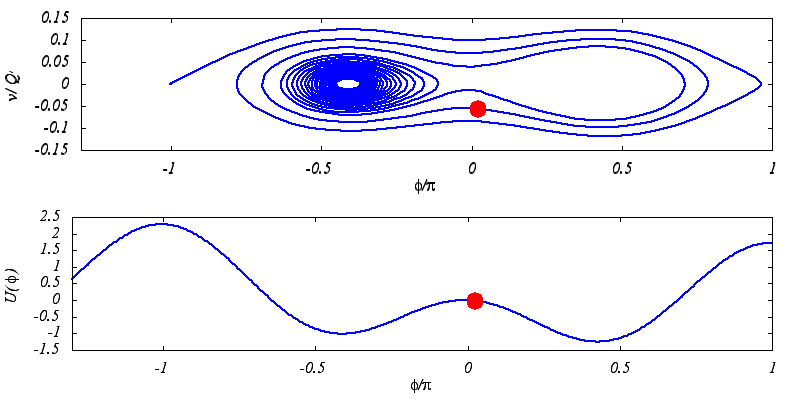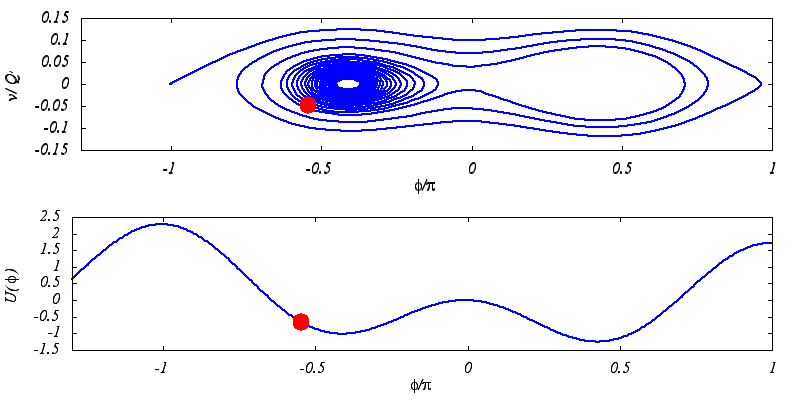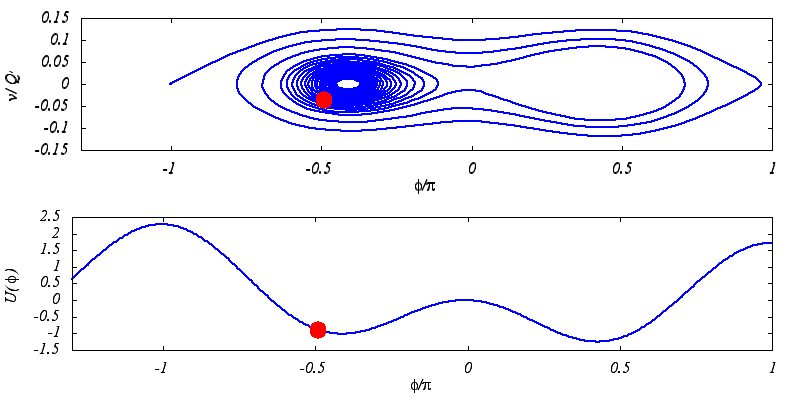Unconventional Josephson junctions can have a current-phase relation I(Φ)=I1sin(Φ)-I2sin(2Φ)
where the second harmonic plays an important role. As a consequence these systems show some interesting properties.
For example they have two escape currents from the superconducting state to the finite voltage state if the damping is low enough.
Similarly, their retrapping trajectories are sensitive to small changes of parameters and can be quite complicated.
This is what the animations illustrate. The lower one is a mechanical analogy of the model that we use to describe the JJs.
It is a particle in a generalized tilted washboard potential. The tilt plays the role of bias current.
The upper animation shows the retrapping trajectory of the particle for a system with low damping.
Note that this is a noiseless scenario. We are interested in a more realistic case where the noise is present in the system
(finite temperatures).Related publication:[1]
Superconducting quantum dot
Superconducting quantum dot (SQD) is a hybrid of two different physical worlds. It consists of a quantum dot, which is basically a device that allows as to store and manipulate single electrons and superconducting leads, where superconductivity is a quantum phenomena with trillions of electrons acting together in the form of condensate. Such a combination leads to a rich playground where meny physical phenomena can be observed and tested in controllable manner. These include quantum phase transitions, Kondo physics, exotic quasi-particles or changing the direction of the current just by manipulating the superconducting phase. Moreover, because SQDs are basically a tunable Josephson junctions, they have a tremendous potential for real world applications.Most of our work which focuses on SQDs has the common denominator in the effort to make the analyses of these complicated structures easier. I have to say that this effort was not without effect.
Dynamical corrections
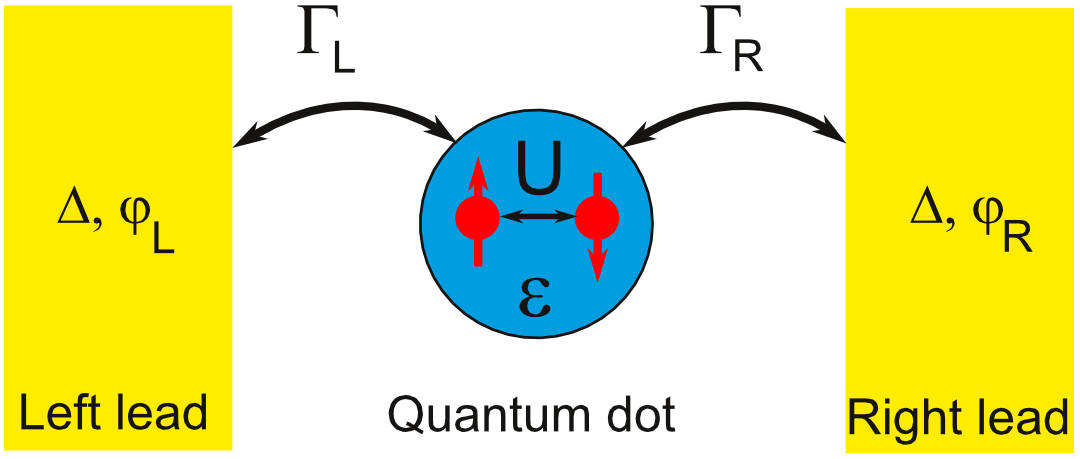We have found out, that a single-level quantum dot (illustration) with Coulomb repulsion (U) attached (Γ)
to two superconducting leads can be studied via the perturbation expansion in the interaction strength.
At zero temperature the second order of the expansion in its spin-symmetric version yields
a nearly perfect agreement with the numerically exact calculations for the position of the 0-π
phase boundary at which the Andreev bound states reach the Fermi energy
as well as for the values of single-particle quantities in the 0-phase.This was kind of a shock to us because theorist usually reckon on much more elaborated techniques or heavy numerics when dealing with this system. We basically showed that for a broad range of parameters, including experimentally relevant ones, a simple textbook method is good enough.
Moreover, we have also found a simple analytical formula for a quick and surprisingly good estimation of the phase boundary in SQD.
We have also tested some more elaborated techniques suitable for other range of parameters. Related publications: [1] [2] [3] [4] [5] [6]
Symmetric - Asymmetric coupling relation
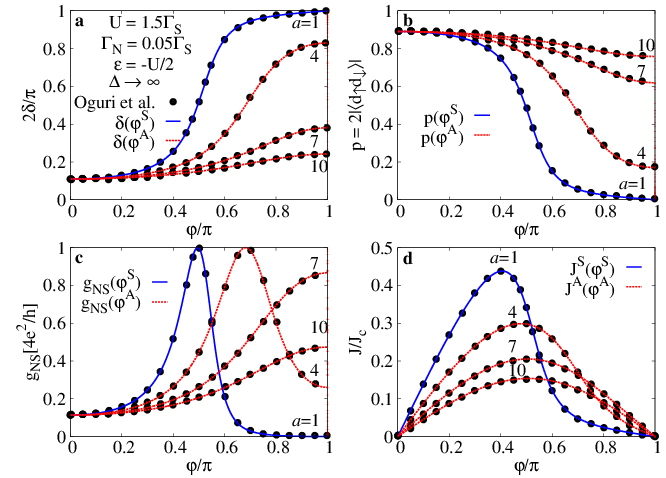This is something that I am really proud of.
In the general case can be the SQD coupled to the left and right electrode asymmetrically.
This is actually a generic situation in the experiments
where the asymmetry plays an important role and what is more it is hard to gain from the data.
Despite this, the theory usually deals only with the symmetric coupling for the sake of simplicity.
We have shoved that not only there exist a simple symmetry relation between
the symmetric and asymmetric coupling, but also that the symmetric coupling is the most general one.
This means that any asymmetric scenario can be extracted in a trivial way from the related
symmetric calculation. Using just a simple formula
any previous calculations of the symmetric case can be immediately extended to asymmetric case.
As a bonus, we have also showed how to use this to simply extract the asymmetry from the experimental
measurements.Related publications: [1]
Phase transitions in the Falicov-Kimball model
The Falicov-Kimball model is to my knowledge the simplest model dealing with the interactions of classical and quantum particles. Despite its simplicity it is applicable to a broad range of problems. It was initially introduced as a limit case of the Hubbard model and independently as a model for the description of metal-insulator phase transitions in rare-earth and transition-metal materials. It has been used to study the crystalization process and it is particularly useful for the description of cold atoms placed in optical lattices. I was studying this model and its various generalizations (including the Hubbard model) during my post-gradual studies by using different numerical methods. We focused mostly on the spin and charge orderings and related phase transition. The aim was to explain the presence of exotic orderings, such as charge strips, in real strongly-correlated systems.My PhD thesis with papers included:[1] (in Slovak)
List of related publications::[2]
Where to find me